Os polinômios, a priori, formam um plano conceitual importante na álgebra, entretanto possuem também uma relevante importância na geometria, quando se deseja calcular expressões que envolvem valores desconhecidos.
A definição de polinômio abrange diversas áreas, pois podemos ter polinômios com apenas um termo na expressão algébrica, como por exemplo: 2x, y, 4z, 2, 5, etc. Mas podemos possuir polinômios com uma infinidade de termos. Por exemplo:
P(x)=an xn+a(n-1) x(n-1)+...+a2 x2+a1 x+a0
Como podemos notar, polinômios são compostos pelas várias expressões algébricas, desde aquelas que envolvem apenas números, até as que apresentam diversas letras, potências, coeficientes, entre outros elementos dos polinômios.
Os polinômios se encontram em um âmbito da matemática denominado álgebra, contudo a álgebra correlaciona o uso de letras, representativas de um número qualquer, com operações aritméticas. Portanto, podemos, assim, efetuar as operações aritméticas nos polinômios, que são: adição, subtração, divisão, multiplicação, potenciação e radiciação.
Buscaremos, então, nesta seção, abarcar todas as propriedades dos polinômios, assim como as operações aritméticas desses números.
Polinômio
Um polinômio qualquer pode ser representado pela expressão:
a0 xn + a1 xn – 1 + a2 xn -2 + ... + an – 1 x + an
A função polinomial será definida por:
P(x) = a0xn + a1xn – 1 + a2xn -2 + ... + an – 1x + an
Com:
a0 , a1 , a2, … , an – 1 e an são números complexos e n.jpg) N.
N.
• Valor numérico de um polinômio
Se observarmos um polinômio qualquer P(x) = 5x4 – 3x3 + x2 – x + 2, para acharmos o seu valor numérico que é o valor de P(x), temos que ter um valor para a incógnita x.
Então, se dissermos que x = 2 o valor que encontrarmos para P(2) quando substituirmos x por 2 será o valor numérico do polinômio.
P(2) = 5 . 24 – 3 . 23 + 22 – 2 + 2
P(2) = 5 . 16 – 3 . 8 + 4 – 2 + 2
P(2) = 80 – 24 + 4
P(2) = 56 + 4
P(2) = 60
Concluímos que o valor numérico do polinômio P(x) = 5x4 – 3x3 + x2 – x + 2, quando
x = 2 será P(2) = 60.
• Raiz ou zero do polinômio
Se pegarmos um polinômio qualquer P(x) = - 2x3 + 5x2 – x + 1 = 0, a raiz dele será um número qualquer b se, somente se, o valor numérico do polinômio for zero quando
x = b.
Exemplo:
P(x) = x2 - 1, para calcularmos o zero da função, devemos colocar P(x) = 0, então:
x2 - 1 = 0
x2 = 1
x = + 1 ou - 1
Concluímos que -1 e +1 é raiz do polinômio P(x) = x2 - 1.
• Grau de um polinômio
Um polinômio é formado por vários monômios separados por operações, então o grau de um polinômio corresponde ao monômio de maior grau. O único polinômio que não possui grau é o polinômio nulo P(x) = 0, por exemplo:
• P(x) = x3 - x2 + 2x -3 → temos 3 monômios que possuem grau, o que tem maior grau é x3, então o polinômio tem o mesmo grau que ele.
P(x) = x3 - x2 + 2x -3 é do 3º grau.
• P(x) = 5x0 = 5 → grau zero.
a0 xn + a1 xn – 1 + a2 xn -2 + ... + an – 1 x + an
A função polinomial será definida por:
P(x) = a0xn + a1xn – 1 + a2xn -2 + ... + an – 1x + an
Com:
a0 , a1 , a2, … , an – 1 e an são números complexos e n
• Valor numérico de um polinômio
Se observarmos um polinômio qualquer P(x) = 5x4 – 3x3 + x2 – x + 2, para acharmos o seu valor numérico que é o valor de P(x), temos que ter um valor para a incógnita x.
Então, se dissermos que x = 2 o valor que encontrarmos para P(2) quando substituirmos x por 2 será o valor numérico do polinômio.
P(2) = 5 . 24 – 3 . 23 + 22 – 2 + 2
P(2) = 5 . 16 – 3 . 8 + 4 – 2 + 2
P(2) = 80 – 24 + 4
P(2) = 56 + 4
P(2) = 60
Concluímos que o valor numérico do polinômio P(x) = 5x4 – 3x3 + x2 – x + 2, quando
x = 2 será P(2) = 60.
• Raiz ou zero do polinômio
Se pegarmos um polinômio qualquer P(x) = - 2x3 + 5x2 – x + 1 = 0, a raiz dele será um número qualquer b se, somente se, o valor numérico do polinômio for zero quando
x = b.
Exemplo:
P(x) = x2 - 1, para calcularmos o zero da função, devemos colocar P(x) = 0, então:
x2 - 1 = 0
x2 = 1
x = + 1 ou - 1
Concluímos que -1 e +1 é raiz do polinômio P(x) = x2 - 1.
• Grau de um polinômio
Um polinômio é formado por vários monômios separados por operações, então o grau de um polinômio corresponde ao monômio de maior grau. O único polinômio que não possui grau é o polinômio nulo P(x) = 0, por exemplo:
• P(x) = x3 - x2 + 2x -3 → temos 3 monômios que possuem grau, o que tem maior grau é x3, então o polinômio tem o mesmo grau que ele.
P(x) = x3 - x2 + 2x -3 é do 3º grau.
• P(x) = 5x0 = 5 → grau zero.
Adição e Subtração de Polinômios
O procedimento utilizado na adição e subtração de polinômios envolve técnicas de redução de termos semelhantes, jogo de sinal, operações envolvendo sinais iguais e sinais diferentes. Observe os exemplos a seguir:
Adição
Exemplo 1
Adicionar x2 – 3x – 1 com –3x2 + 8x – 6.
(x2 – 3x – 1) + (–3x2 + 8x – 6) → eliminar o segundo parênteses através do jogo de sinal.
+(–3x2) = –3x2
+(+8x) = +8x
+(–6) = –6
x2 – 3x – 1 –3x2 + 8x – 6 → reduzir os termos semelhantes.
x2 – 3x2 – 3x + 8x – 1 – 6
–2x2 + 5x – 7
Portanto: (x2 – 3x – 1) + (–3x2 + 8x – 6) = –2x2 + 5x – 7
Exemplo 2
Adicionando 4x2 – 10x – 5 e 6x + 12, teremos:
(4x2 – 10x – 5) + (6x + 12) → eliminar os parênteses utilizando o jogo de sinal.
4x2 – 10x – 5 + 6x + 12 → reduzir os termos semelhantes.
4x2 – 10x + 6x – 5 + 12
4x2 – 4x + 7
Portanto: (4x2 – 10x – 5) + (6x + 12) = 4x2 – 4x + 7
Subtração
Exemplo 3
Subtraindo –3x2 + 10x – 6 de 5x2 – 9x – 8.
(5x2 – 9x – 8) – (–3x2 + 10x – 6) → eliminar os parênteses utilizando o jogo de sinal.
– (–3x2) = +3x2
– (+10x) = –10x
– (–6) = +6
5x2 – 9x – 8 + 3x2 –10x +6 → reduzir os termos semelhantes.
5x2 + 3x2 – 9x –10x – 8 + 6
8x2 – 19x – 2
Portanto: (5x2 – 9x – 8) – (–3x2 + 10x – 6) = 8x2 – 19x – 2
Exemplo 4
Se subtrairmos 2x³ – 5x² – x + 21 e 2x³ + x² – 2x + 5, teremos:
(2x³ – 5x² – x + 21) – (2x³ + x² – 2x + 5) → eliminando os parênteses através do jogo de sinais.
2x³ – 5x² – x + 21 – 2x³ – x² + 2x – 5 → redução de termos semelhantes.
2x³ – 2x³ – 5x² – x² – x + 2x + 21 – 5
0x³ – 6x² + x + 16
– 6x² + x + 16
Portanto: (2x³ – 5x² – x + 21) – (2x³ + x² – 2x + 5) = – 6x² + x + 16
Exemplo 5
Considerando os polinômios A = 6x³ + 5x² – 8x + 15, B = 2x³ – 6x² – 9x + 10 e C = x³ + 7x² + 9x + 20. Calcule:
a) A + B + C
(6x³ + 5x² – 8x + 15) + (2x³ – 6x² – 9x + 10) + (x³ + 7x² + 9x + 20)
6x³ + 5x² – 8x + 15 + 2x³ – 6x² – 9x + 10 + x³ + 7x² + 9x + 20
6x³ + 2x³ + x³ + 5x² – 6x² + 7x² – 8x – 9x + 9x + 15 + 10 + 20
9x³ + 6x² – 8x + 45
A + B + C = 9x³ + 6x² – 8x + 45
b) A – B – C
(6x³ + 5x² – 8x + 15) – (2x³ – 6x² – 9x + 10) – (x³ + 7x² + 9x + 20)
6x³ + 5x² – 8x + 15 – 2x³ + 6x² + 9x – 10 – x³ – 7x² – 9x – 20
6x³ – 2x³ – x³ + 5x² + 6x² – 7x² – 8x + 9x – 9x + 15 – 10 – 20
6x³ – 3x³ + 11x² – 7x² – 17x + 9x + 15 – 30
3x³ + 4x² – 8x – 15
A – B – C = 3x³ + 4x² – 8x – 15
Adição
Exemplo 1
Adicionar x2 – 3x – 1 com –3x2 + 8x – 6.
(x2 – 3x – 1) + (–3x2 + 8x – 6) → eliminar o segundo parênteses através do jogo de sinal.
+(–3x2) = –3x2
+(+8x) = +8x
+(–6) = –6
x2 – 3x – 1 –3x2 + 8x – 6 → reduzir os termos semelhantes.
x2 – 3x2 – 3x + 8x – 1 – 6
–2x2 + 5x – 7
Portanto: (x2 – 3x – 1) + (–3x2 + 8x – 6) = –2x2 + 5x – 7
Exemplo 2
Adicionando 4x2 – 10x – 5 e 6x + 12, teremos:
(4x2 – 10x – 5) + (6x + 12) → eliminar os parênteses utilizando o jogo de sinal.
4x2 – 10x – 5 + 6x + 12 → reduzir os termos semelhantes.
4x2 – 10x + 6x – 5 + 12
4x2 – 4x + 7
Portanto: (4x2 – 10x – 5) + (6x + 12) = 4x2 – 4x + 7
Subtração
Exemplo 3
Subtraindo –3x2 + 10x – 6 de 5x2 – 9x – 8.
(5x2 – 9x – 8) – (–3x2 + 10x – 6) → eliminar os parênteses utilizando o jogo de sinal.
– (–3x2) = +3x2
– (+10x) = –10x
– (–6) = +6
5x2 – 9x – 8 + 3x2 –10x +6 → reduzir os termos semelhantes.
5x2 + 3x2 – 9x –10x – 8 + 6
8x2 – 19x – 2
Portanto: (5x2 – 9x – 8) – (–3x2 + 10x – 6) = 8x2 – 19x – 2
Exemplo 4
Se subtrairmos 2x³ – 5x² – x + 21 e 2x³ + x² – 2x + 5, teremos:
(2x³ – 5x² – x + 21) – (2x³ + x² – 2x + 5) → eliminando os parênteses através do jogo de sinais.
2x³ – 5x² – x + 21 – 2x³ – x² + 2x – 5 → redução de termos semelhantes.
2x³ – 2x³ – 5x² – x² – x + 2x + 21 – 5
0x³ – 6x² + x + 16
– 6x² + x + 16
Portanto: (2x³ – 5x² – x + 21) – (2x³ + x² – 2x + 5) = – 6x² + x + 16
Exemplo 5
Considerando os polinômios A = 6x³ + 5x² – 8x + 15, B = 2x³ – 6x² – 9x + 10 e C = x³ + 7x² + 9x + 20. Calcule:
a) A + B + C
(6x³ + 5x² – 8x + 15) + (2x³ – 6x² – 9x + 10) + (x³ + 7x² + 9x + 20)
6x³ + 5x² – 8x + 15 + 2x³ – 6x² – 9x + 10 + x³ + 7x² + 9x + 20
6x³ + 2x³ + x³ + 5x² – 6x² + 7x² – 8x – 9x + 9x + 15 + 10 + 20
9x³ + 6x² – 8x + 45
A + B + C = 9x³ + 6x² – 8x + 45
b) A – B – C
(6x³ + 5x² – 8x + 15) – (2x³ – 6x² – 9x + 10) – (x³ + 7x² + 9x + 20)
6x³ + 5x² – 8x + 15 – 2x³ + 6x² + 9x – 10 – x³ – 7x² – 9x – 20
6x³ – 2x³ – x³ + 5x² + 6x² – 7x² – 8x + 9x – 9x + 15 – 10 – 20
6x³ – 3x³ + 11x² – 7x² – 17x + 9x + 15 – 30
3x³ + 4x² – 8x – 15
A – B – C = 3x³ + 4x² – 8x – 15
Adição, Subtração e Multiplicação de Polinômios
Nas situações envolvendo cálculos algébricos, é de extrema importância a aplicação de regras nas operações entre os monômios. As situações aqui apresentadas abordarão a adição, a subtração e a multiplicação de polinômios.
Adição e Subtração
Considere os polinômios –2x² + 5x – 2 e –3x³ + 2x – 1. Vamos efetuar a adição e a subtração entre eles.
Adição
(–2x² + 5x – 2) + (–3x³ + 2x – 1) → eliminar os parênteses realizando o jogo de sinal
–2x² + 5x – 2 – 3x³ + 2x – 1 → reduzir os termos semelhantes
–2x² + 7x – 3x³ – 3 → ordenar de forma decrescente de acordo com a potência
–3x³ – 2x² + 7x – 3
Subtração
(–2x² + 5x – 2) – (–3x³ + 2x – 1) → eliminar os parênteses realizando o jogo de sinal
–2x² + 5x – 2 + 3x³ – 2x + 1 → reduzir os termos semelhantes
–2x² + 3x – 1 + 3x³ → ordenar de forma decrescente de acordo com a potência
3x³ – 2x² + 3x – 1
Multiplicação de polinômio por monômio
Para entendermos melhor, observe o exemplo:
(3x2) * (5x3 + 8x2 – x) → aplicar a propriedade distributiva da multiplicação
15x5 + 24x4 – 3x3
Multiplicação de polinômio por polinômio
Para efetuarmos a multiplicação de polinômio por polinômio também devemos utilizar a propriedade distributiva. Veja o exemplo:
(x – 1) * (x2 + 2x - 6)
x2 * (x – 1) + 2x * (x – 1) – 6 * (x – 1)
(x³ – x²) + (2x² – 2x) – (6x – 6)
x³ – x² + 2x² – 2x – 6x + 6 → reduzindo os termos semelhantes.
x³ + x² – 8x + 6
Portanto, nas multiplicações entre monômios e polinômios aplicamos a propriedade distributiva da multiplicação.
Adição e Subtração
Considere os polinômios –2x² + 5x – 2 e –3x³ + 2x – 1. Vamos efetuar a adição e a subtração entre eles.
Adição
(–2x² + 5x – 2) + (–3x³ + 2x – 1) → eliminar os parênteses realizando o jogo de sinal
–2x² + 5x – 2 – 3x³ + 2x – 1 → reduzir os termos semelhantes
–2x² + 7x – 3x³ – 3 → ordenar de forma decrescente de acordo com a potência
–3x³ – 2x² + 7x – 3
Subtração
(–2x² + 5x – 2) – (–3x³ + 2x – 1) → eliminar os parênteses realizando o jogo de sinal
–2x² + 5x – 2 + 3x³ – 2x + 1 → reduzir os termos semelhantes
–2x² + 3x – 1 + 3x³ → ordenar de forma decrescente de acordo com a potência
3x³ – 2x² + 3x – 1
Multiplicação de polinômio por monômio
Para entendermos melhor, observe o exemplo:
(3x2) * (5x3 + 8x2 – x) → aplicar a propriedade distributiva da multiplicação
15x5 + 24x4 – 3x3
Multiplicação de polinômio por polinômio
Para efetuarmos a multiplicação de polinômio por polinômio também devemos utilizar a propriedade distributiva. Veja o exemplo:
(x – 1) * (x2 + 2x - 6)
x2 * (x – 1) + 2x * (x – 1) – 6 * (x – 1)
(x³ – x²) + (2x² – 2x) – (6x – 6)
x³ – x² + 2x² – 2x – 6x + 6 → reduzindo os termos semelhantes.
x³ + x² – 8x + 6
Portanto, nas multiplicações entre monômios e polinômios aplicamos a propriedade distributiva da multiplicação.
Demonstrações através do cálculo algébrico
No estudo sobre o cálculo algébrico aprendemos a operar polinômios, fazer a sua fatoração e encontrar o seu mmc. E com essas informações é possível fazer algumas demonstrações como:
• A soma de dois números inteiros consecutivos será sempre a diferença de seus quadrados.
Considere x como sendo um número inteiro qualquer, o seu sucessor pode ser representado pelo polinômio x + 1. Somando esses dois polinômios chegaremos à seguinte expressão algébrica:
x + (x + 1) = x + x + 1 = 2x + 1
A diferença dos quadrados desses dois números consecutivos será representada pela seguinte expressão algébrica:
(x +1)2 - x2 = (x2 + 2x + 1) – x2 = x2 + 2x + 1 - x2 = 2x + 1
Comparado as duas expressões algébricas encontradas, podemos confirmar que
x + (x + 1) = (x +1)2 - x2
• A soma de cinco números inteiros consecutivos será sempre múltiplo de 5.
Considere como sendo cinco números inteiros consecutivos os polinômios: x-2 ; x-1 ; x ; x + 1 ; x + 2.
Um número para que seja múltiplo de cinco pode ser escrito da seguinte forma: 5x, onde x é um número inteiro qualquer, ou seja, qualquer número que multiplicado por 5 será múltiplo de cinco.
Somando os cinco números consecutivos teremos:
x - 2 + x - 1 + x + x + 1 + x + 2 = 5x -3 + 3 = 5x, portanto, é verdadeiro dizer que a soma de 5 números inteiros consecutivos terá como resposta um número múltiplo de 5.
• A soma de dois números inteiros ímpares será sempre um número par.
Para que um número seja par é preciso que ele esteja escrito da seguinte forma: 2x, onde x representa um número inteiro qualquer. Dessa forma, um número ímpar seria igual a 2x +1.
Somar dois números ímpares seria o mesmo que:
(2x +1) + (2x + 1) = 2 (2x + 1). A expressão algébrica (2x + 1) terá valor numérico igual a um número inteiro qualquer, quando multiplicado por 2 (2x + 1) irá resultar em um número par.
• A soma de dois números inteiros consecutivos será sempre a diferença de seus quadrados.
Considere x como sendo um número inteiro qualquer, o seu sucessor pode ser representado pelo polinômio x + 1. Somando esses dois polinômios chegaremos à seguinte expressão algébrica:
x + (x + 1) = x + x + 1 = 2x + 1
A diferença dos quadrados desses dois números consecutivos será representada pela seguinte expressão algébrica:
(x +1)2 - x2 = (x2 + 2x + 1) – x2 = x2 + 2x + 1 - x2 = 2x + 1
Comparado as duas expressões algébricas encontradas, podemos confirmar que
x + (x + 1) = (x +1)2 - x2
• A soma de cinco números inteiros consecutivos será sempre múltiplo de 5.
Considere como sendo cinco números inteiros consecutivos os polinômios: x-2 ; x-1 ; x ; x + 1 ; x + 2.
Um número para que seja múltiplo de cinco pode ser escrito da seguinte forma: 5x, onde x é um número inteiro qualquer, ou seja, qualquer número que multiplicado por 5 será múltiplo de cinco.
Somando os cinco números consecutivos teremos:
x - 2 + x - 1 + x + x + 1 + x + 2 = 5x -3 + 3 = 5x, portanto, é verdadeiro dizer que a soma de 5 números inteiros consecutivos terá como resposta um número múltiplo de 5.
• A soma de dois números inteiros ímpares será sempre um número par.
Para que um número seja par é preciso que ele esteja escrito da seguinte forma: 2x, onde x representa um número inteiro qualquer. Dessa forma, um número ímpar seria igual a 2x +1.
Somar dois números ímpares seria o mesmo que:
(2x +1) + (2x + 1) = 2 (2x + 1). A expressão algébrica (2x + 1) terá valor numérico igual a um número inteiro qualquer, quando multiplicado por 2 (2x + 1) irá resultar em um número par.
Divisão de polinômio por polinômio
Em toda divisão temos dividendo, divisor, quociente e resto, como estamos falando de divisão de polinômio por polinômio, teremos:
Para o dividendo um polinômio G(x)
Para o divisor um polinômio D(x)
Para o quociente um polinômio Q(x)Para o resto (podendo ser zero) um polinômio R(x)

Prova real:
Tem algumas observações a serem feitas, como:
? ao final da divisão o resto sempre tem que ser menor que o divisor: R(x) < D(x).
? quando o resto for igual a zero, a divisão é considerada exata, ou seja, o dividendo é divisível pelo divisor. R(x) = 0.
Observe a divisão de polinômio por polinômio abaixo, vamos partir de um exemplo, cada passo tomado no desenvolvimento da divisão será explicado.
Dada a divisão
(12x3 + 9 – 4x) : (x + 2x2 + 3)
Antes de começar a operação temos que fazer algumas verificações:
? se todos os polinômios estão em ordem conforme as potências de x.
No caso da nossa divisão devemos ordenar, ficando assim:
(12x3 - 4x + 9) : (2x2 + x + 3)
? observar se no polinômio G(x) não está faltando algum termo, se estiver devemos completar.
No polinômio 12x3 - 4x + 9 está faltando o termo x2, completando ficará assim:
12x3 + 0x2 - 4x + 9
Agora podemos iniciar a divisão:
.jpg)
? G(x) tem 3 termos e D(x) tem 3 termos. Pegamos o 1º termo de G(x) e dividimos pelo 1º termo de D(x): 12x3 : 2x2 = 6x, o resultado multiplicará o polinômio 2x2+ x + 3 e o resultado dessa multiplicação subtrairemos pelo polinômio 12x3 + 0x2 - 4x + 9. Assim teremos:
.jpg)

? R(x) > D(x), podemos dar continuidade à divisão, repetindo o mesmo processo anterior. Achando agora o segundo termo de Q(x).
.jpg)
.jpg)
R(x) < D(x), não damos continuidade a divisão, concluindo que:
O quociente é 6x – 3 e o resto é –19x + 18.
.jpg)
.jpg)
.jpg)
.jpg)
Para o dividendo um polinômio G(x)
Para o divisor um polinômio D(x)
Para o quociente um polinômio Q(x)Para o resto (podendo ser zero) um polinômio R(x)
Prova real:
Tem algumas observações a serem feitas, como:
? ao final da divisão o resto sempre tem que ser menor que o divisor: R(x) < D(x).
? quando o resto for igual a zero, a divisão é considerada exata, ou seja, o dividendo é divisível pelo divisor. R(x) = 0.
Observe a divisão de polinômio por polinômio abaixo, vamos partir de um exemplo, cada passo tomado no desenvolvimento da divisão será explicado.
Dada a divisão
(12x3 + 9 – 4x) : (x + 2x2 + 3)
Antes de começar a operação temos que fazer algumas verificações:
? se todos os polinômios estão em ordem conforme as potências de x.
No caso da nossa divisão devemos ordenar, ficando assim:
(12x3 - 4x + 9) : (2x2 + x + 3)
? observar se no polinômio G(x) não está faltando algum termo, se estiver devemos completar.
No polinômio 12x3 - 4x + 9 está faltando o termo x2, completando ficará assim:
12x3 + 0x2 - 4x + 9
Agora podemos iniciar a divisão:
? G(x) tem 3 termos e D(x) tem 3 termos. Pegamos o 1º termo de G(x) e dividimos pelo 1º termo de D(x): 12x3 : 2x2 = 6x, o resultado multiplicará o polinômio 2x2+ x + 3 e o resultado dessa multiplicação subtrairemos pelo polinômio 12x3 + 0x2 - 4x + 9. Assim teremos:
? R(x) > D(x), podemos dar continuidade à divisão, repetindo o mesmo processo anterior. Achando agora o segundo termo de Q(x).
.jpg)
R(x) < D(x), não damos continuidade a divisão, concluindo que:
O quociente é 6x – 3 e o resto é –19x + 18.
Divisão de polinômios
Polinômio é uma expressão algébrica composta por dois ou mais monômios. Na divisão de polinômios, utilizamos duas regras matemáticas fundamentais: realizar a divisão entre os coeficientes numéricos e divisão de potências de mesma base (conservar a base e subtrair os expoentes).
Quando trabalhamos com divisão, utilizamos também a multiplicação no processo. Observe o seguinte esquema:
Quando trabalhamos com divisão, utilizamos também a multiplicação no processo. Observe o seguinte esquema:
.jpg)
Vamos dividir um polinômio por um monômio, com o intuito de entendermos o processo operatório. Observe:
Exemplo 1:
Exemplo 1:
.jpg)
Caso queira verificar se a divisão está correta, basta multiplicar o quociente pelo divisor, com vistas a obter o dividendo como resultado.
Verificando → quociente * divisor + resto = dividendo4x * (3x² + x – 2) + 0
12x³ + 4x² – 8x
Caso isso ocorra, a divisão está correta. No exemplo a seguir, iremos dividir polinômio por polinômio. Veja:
Exemplo 2:
Verificando → quociente * divisor + resto = dividendo4x * (3x² + x – 2) + 0
12x³ + 4x² – 8x
Caso isso ocorra, a divisão está correta. No exemplo a seguir, iremos dividir polinômio por polinômio. Veja:
Exemplo 2:
.jpg)
Verificando → quociente * divisor + resto = dividendo(2x – 5) * (5x – 9) + (–5)
10x² – 18x – 25x + 45 + (–5)
10x² – 43x + 45 – 5
10x² – 43x + 40
Observe o exemplo de número 3:
10x² – 18x – 25x + 45 + (–5)
10x² – 43x + 45 – 5
10x² – 43x + 40
Observe o exemplo de número 3:
.jpg)
Verificando → quociente * divisor + resto = dividendo
(3x² + x – 1) * (2x² – 4x + 5) + 0
6x4 – 12x³ + 15x² + 2x³ – 4x² + 5x – 2x² + 4x – 5
6x4 – 10x³ + 9x² + 9x – 5
Exemplo 4:
.jpg)
(3x² + x – 1) * (2x² – 4x + 5) + 0
6x4 – 12x³ + 15x² + 2x³ – 4x² + 5x – 2x² + 4x – 5
6x4 – 10x³ + 9x² + 9x – 5
Exemplo 4:
.jpg)
Verificando → quociente * divisor + resto = dividendo
(4x – 5) * (3x² – x + 2) + (2x + 7)
12x³ – 4x² + 8x – 15x² + 5x – 10 + (2x + 7)
12x³ – 19x² + 13x – 10 + 2x + 7
12x³ – 19x² + 15x – 3
(4x – 5) * (3x² – x + 2) + (2x + 7)
12x³ – 4x² + 8x – 15x² + 5x – 10 + (2x + 7)
12x³ – 19x² + 13x – 10 + 2x + 7
12x³ – 19x² + 15x – 3
Divisão de Polinômios utilizando o dispositivo de Briot-Ruffini
Compreendendo um dispositivo que auxilia na divisão de polinômios: o dispositivo de Briot-Ruffini. Esse dispositivo utiliza uma raiz do polinômio e seus coeficientes para calcular a divisão do polinômio pela sua raiz.
Podemos ver no artigo de Divisão de polinômios o método tradicional para a divisão, utilizando o algoritmo da divisão. Entretanto, dois matemáticos (Paolo Ruffini e A. Briot) criaram um dispositivo prático para realizar esta divisão, dispositivo este que recebeu seus nomes: dispositivo de Briot-Ruffini.
Esse algoritmo é utilizado para dividirmos polinômios por um binômio do tipo (x-a). Esse dispositivo usará apenas os coeficientes do polinômio e o termo constante (a).
Chamemos de p(x) o polinômio a ser dividido (dividendo); e h(x) o divisor no qual h(x)=x-a. Com isso, a estrutura do dispositivo é a seguinte:
.JPG)
Para melhor compreendermos como este dispositivo funciona, utilizá-lo-emos em um exemplo, e explicaremos passo a passo seu processo.
Exemplo:
Efetue a divisão de p(x) por h(x), na qual:
.png)

Agora multiplique esse termo repetido pelo divisor, o resultado será somado ao próximo termo do dividendo p(x).

Repita o processo agora para o novo elemento, multiplique esse número pelo divisor e some-o ao próximo termo.
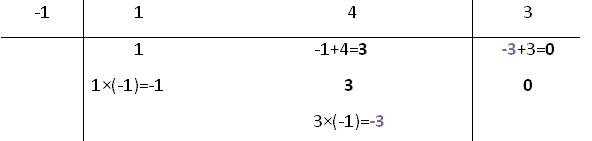
Obtemos o resto 0 e um quociente da seguinte forma:
.png)
.png)
.png)
.jpg)
Esse algoritmo é utilizado para dividirmos polinômios por um binômio do tipo (x-a). Esse dispositivo usará apenas os coeficientes do polinômio e o termo constante (a).
Chamemos de p(x) o polinômio a ser dividido (dividendo); e h(x) o divisor no qual h(x)=x-a. Com isso, a estrutura do dispositivo é a seguinte:
.JPG)
Para melhor compreendermos como este dispositivo funciona, utilizá-lo-emos em um exemplo, e explicaremos passo a passo seu processo.
Exemplo:
Efetue a divisão de p(x) por h(x), na qual:
.png)

Agora multiplique esse termo repetido pelo divisor, o resultado será somado ao próximo termo do dividendo p(x).

Repita o processo agora para o novo elemento, multiplique esse número pelo divisor e some-o ao próximo termo.
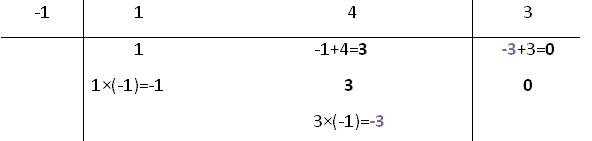
Obtemos o resto 0 e um quociente da seguinte forma:
.png)
Para verificarmos se a divisão foi feita de forma correta, podemos utilizar o algoritmo da divisão que diz o seguinte:
.png)
Dessa forma, temos:
.png)
Logo, a divisão foi feita corretamente, pois ao verificar os termos da divisão no algoritmo da divisão constatamos que a igualdade é verdadeira.
Equação Polinomial
Equação polinomial ou algébrica é toda equação da forma p(x) = 0, em que p(x) é um polinômio:
p(x) = anxn + an-1xn-1 + ... + a1x + a0 de grau n, com n ≥ 1. Veja alguns exemplos:
x4 + 9x2 – 10x + 3 = 0
10x6 – 2x5 + 6x4 + 12x3 – x2 + x + 7 = 0
x8 – x6 – 6x + 2 = 0
x10 – 6x2 + 9 = 0
As raízes de uma equação polinomial constituem o conjunto solução da equação. Para as equações em que o grau é 1 ou 2, o método de resolução é simples e prático. Nos casos em que o grau dos polinômios é 3 ou 4, existem expressões para a obtenção da solução.
Teorema Fundamental da Álgebra (TFA)
Toda equação polinomial p(x) = 0, de grau n onde n ≥ 1, admite pelo menos uma raiz complexa.
Exemplo 1
Determine o valor do coeficiente K, sabendo que 2 é a raiz da equação:
2x4 + kx3 – 5x2 + x – 15 = 0
Se 2 é raiz da equação, então temos:
2(2)4 + k(2)3 – 5(2)2 + 2 – 15 = 0
2*16 + k*8 – 5*4 + 2 – 15 = 0
32 + 8k – 20 + 2 – 15 = 0
8k + 34 – 35 = 0
8k – 1 = 0
8k = 1
k = 1/8
Temos que o valor do coeficiente k é 1/8.
Exemplo 2
Determine o valor de m, sabendo que –3 é raiz da equação: mx3 + (m + 2)x2 – 3x – m – 8 = 0.
Temos que:
m(–3)3 + (m + 2)( –3)2 – 3(–3) – m – 8 = 0
m(–27) + (m + 2)(9) + 9 – m – 8 = 0
–27m + 9m + 18 + 9 – m – 8 = 0
–27m + 9m – m = 8 – 18 – 9
– 19m = –19
m = 1
O valor de m é 1.
p(x) = anxn + an-1xn-1 + ... + a1x + a0 de grau n, com n ≥ 1. Veja alguns exemplos:
x4 + 9x2 – 10x + 3 = 0
10x6 – 2x5 + 6x4 + 12x3 – x2 + x + 7 = 0
x8 – x6 – 6x + 2 = 0
x10 – 6x2 + 9 = 0
As raízes de uma equação polinomial constituem o conjunto solução da equação. Para as equações em que o grau é 1 ou 2, o método de resolução é simples e prático. Nos casos em que o grau dos polinômios é 3 ou 4, existem expressões para a obtenção da solução.
Teorema Fundamental da Álgebra (TFA)
Toda equação polinomial p(x) = 0, de grau n onde n ≥ 1, admite pelo menos uma raiz complexa.
Exemplo 1
Determine o valor do coeficiente K, sabendo que 2 é a raiz da equação:
2x4 + kx3 – 5x2 + x – 15 = 0
Se 2 é raiz da equação, então temos:
2(2)4 + k(2)3 – 5(2)2 + 2 – 15 = 0
2*16 + k*8 – 5*4 + 2 – 15 = 0
32 + 8k – 20 + 2 – 15 = 0
8k + 34 – 35 = 0
8k – 1 = 0
8k = 1
k = 1/8
Temos que o valor do coeficiente k é 1/8.
Exemplo 2
Determine o valor de m, sabendo que –3 é raiz da equação: mx3 + (m + 2)x2 – 3x – m – 8 = 0.
Temos que:
m(–3)3 + (m + 2)( –3)2 – 3(–3) – m – 8 = 0
m(–27) + (m + 2)(9) + 9 – m – 8 = 0
–27m + 9m + 18 + 9 – m – 8 = 0
–27m + 9m – m = 8 – 18 – 9
– 19m = –19
m = 1
O valor de m é 1.
Mínimo Múltiplo Comum de Polinômios
As expressões algébricas fracionárias são aquelas em que o denominador possui letras, isto é, termos variáveis. Veja os exemplos:
.jpg)
No caso dessas frações algébricas, antes de realizarmos a soma devemos aplicar o cálculo do mmc, no intuito de igualar os denominadores, pois sabemos que somente adicionamos frações com denominadores iguais.
Para determinarmos o mmc de polinômios, fatoramos cada polinômio individualmente, e logo em seguida multiplicamos todos os fatores sem repetição dos comuns. A utilização dos casos de fatoração é de extrema importância para a determinação de algumas situações envolvendo mmc. Observe o cálculo do mmc entre polinômios nos exemplos a seguir:
Exemplo 1
mmc entre 10x e 5x² – 15x
10x = 2 * 5 * x
5x² – 15x = 5x * (x – 3)
mmc = 2 * 5 * x * (x – 3) = 10x * (x – 3) ou 10x² – 30x
Exemplo 2
mmc entre 6x e 2x³ + 10x²
6x = 2 * 3 * x
2x³ + 10x² = 2x² * (x + 5)
mmc = 2 * 3 * x² * (x + 5) = 6x² * (x + 5) ou 6x³ + 30x²
Exemplo 3
mmc entre x² – 3x + xy – 3y e x² – y²
x² – 3x + xy – 3y = x(x – 3) + y(x – 3) = (x + y) * (x – 3)
x² – y² = (x + y) * (x – y)
mmc = (x – 3) * (x + y) * (x – y)
Exemplo 4
mmc entre x³ + 8 e do trinômio x² + 4x + 4.
x³ + 8 = (x + 2) * (x² – 2x + 4).
x² + 4x + 4 = (x + 2)²
mmc = (x + 2)² * (x² – 2x + 4)
Para determinarmos o mmc de polinômios, fatoramos cada polinômio individualmente, e logo em seguida multiplicamos todos os fatores sem repetição dos comuns. A utilização dos casos de fatoração é de extrema importância para a determinação de algumas situações envolvendo mmc. Observe o cálculo do mmc entre polinômios nos exemplos a seguir:
Exemplo 1
mmc entre 10x e 5x² – 15x
10x = 2 * 5 * x
5x² – 15x = 5x * (x – 3)
mmc = 2 * 5 * x * (x – 3) = 10x * (x – 3) ou 10x² – 30x
Exemplo 2
mmc entre 6x e 2x³ + 10x²
6x = 2 * 3 * x
2x³ + 10x² = 2x² * (x + 5)
mmc = 2 * 3 * x² * (x + 5) = 6x² * (x + 5) ou 6x³ + 30x²
Exemplo 3
mmc entre x² – 3x + xy – 3y e x² – y²
x² – 3x + xy – 3y = x(x – 3) + y(x – 3) = (x + y) * (x – 3)
x² – y² = (x + y) * (x – y)
mmc = (x – 3) * (x + y) * (x – y)
Exemplo 4
mmc entre x³ + 8 e do trinômio x² + 4x + 4.
x³ + 8 = (x + 2) * (x² – 2x + 4).
x² + 4x + 4 = (x + 2)²
mmc = (x + 2)² * (x² – 2x + 4)
Multiplicidade de uma raiz
Na resolução da equação do 2º grau x2 – 6x + 9 = 0, encontramos duas raízes iguais a 3. Utilizando o teorema da decomposição, fatoramos o polinômio e obtemos:
x2 – 6x + 9 = 0 = (x – 3)(x – 3) = (x – 3)2
Nesse caso, dizemos que 3 é raiz de multiplicidade 2 ou raiz dupla da equação.
Dessa forma, se um polinômio fatorado resulta a seguinte expressão:

Podemos dizer que:
x = -5 é raiz com multiplicidade 3 ou raiz tripla da equação p(x) = 0
x = -4 é raiz com multiplicidade 2 ou raiz dupla da equação p(x) = 0
x = 2 é raiz com multiplicidade 1 ou raiz simples da equação p(x) = 0
De maneira geral, dizemos que r é uma raiz de multiplicidade n, com n ≥ 1, da equação p(x) = 0, se:

Observe que p(x) é divisível por (x – r)m e que a condição q(r) ≠ 0 significa que r não é raiz de q(x) e garante que a multiplicidade da raiz r não é maior que m.
Exemplo 1. Resolva a equação x4 – 9x3 + 23x2 – 3x – 36 = 0, sabendo que 3 é raiz dupla.
Solução: considere p(x) como sendo o polinômio dado. Assim:

Note que q(x) é obtido fazendo a divisão de p(x) por (x – 3)2.
Fazendo a divisão pelo dispositivo prático de Briot –Ruffini, obtemos:

Após a realização da divisão, vemos que os coeficientes do polinômio q(x) são 1, -3 e -4. Assim, q(x) = 0 será: x2 – 3x – 4 = 0
Vamos resolver a equação acima para determinarmos as demais raízes.
x2 – 3x – 4 = 0
Δ = (-3)2 - 4*1*(-4)
Δ = 25
x = -1 ou x = 4
Portanto, S = {-1, 3, 4}
Exemplo 2. Escreva uma equação algébrica de grau mínimo tal que 2 seja raiz dupla e – 1, raiz simples.
Solução: Temos que:
(x – 2)(x – 2 )(x – (-1)) = 0
Ou

x2 – 6x + 9 = 0 = (x – 3)(x – 3) = (x – 3)2
Nesse caso, dizemos que 3 é raiz de multiplicidade 2 ou raiz dupla da equação.
Dessa forma, se um polinômio fatorado resulta a seguinte expressão:

Podemos dizer que:
x = -5 é raiz com multiplicidade 3 ou raiz tripla da equação p(x) = 0
x = -4 é raiz com multiplicidade 2 ou raiz dupla da equação p(x) = 0
x = 2 é raiz com multiplicidade 1 ou raiz simples da equação p(x) = 0
De maneira geral, dizemos que r é uma raiz de multiplicidade n, com n ≥ 1, da equação p(x) = 0, se:

Observe que p(x) é divisível por (x – r)m e que a condição q(r) ≠ 0 significa que r não é raiz de q(x) e garante que a multiplicidade da raiz r não é maior que m.
Exemplo 1. Resolva a equação x4 – 9x3 + 23x2 – 3x – 36 = 0, sabendo que 3 é raiz dupla.
Solução: considere p(x) como sendo o polinômio dado. Assim:

Note que q(x) é obtido fazendo a divisão de p(x) por (x – 3)2.
Fazendo a divisão pelo dispositivo prático de Briot –Ruffini, obtemos:

Após a realização da divisão, vemos que os coeficientes do polinômio q(x) são 1, -3 e -4. Assim, q(x) = 0 será: x2 – 3x – 4 = 0
Vamos resolver a equação acima para determinarmos as demais raízes.
x2 – 3x – 4 = 0
Δ = (-3)2 - 4*1*(-4)
Δ = 25
x = -1 ou x = 4
Portanto, S = {-1, 3, 4}
Exemplo 2. Escreva uma equação algébrica de grau mínimo tal que 2 seja raiz dupla e – 1, raiz simples.
Solução: Temos que:
(x – 2)(x – 2 )(x – (-1)) = 0
Ou

Teorema de D’Alembert
O teorema de D’Alembert é uma consequência imediata do teorema do resto, que são voltados para a divisão de polinômio por binômio do tipo x – a. O teorema do resto diz que um polinômio G(x) dividido por um binômio x – a terá resto R igual a P(a), para
x = a. O matemático francês D’Alembert provou, levando em consideração o teorema citado acima, que um polinômio qualquer Q(x) será divisível por x – a, ou seja, o resto da divisão será igual à zero (R = 0) se P(a) = 0.
Esse teorema facilitou o cálculo da divisão de polinômio por binômio (x –a), dessa forma não sendo preciso resolver toda a divisão para saber se o resto é igual ou diferente de zero.
Exemplo 1
Calcule o resto da divisão (x2 + 3x – 10) : (x – 3).
Como diz o Teorema de D’Alembert, o resto (R) dessa divisão será igual a:
P(3) = R
32 + 3 * 3 – 10 = R
9 + 9 – 10 = R
18 – 10 = R
R = 8
Portanto, o resto dessa divisão será 8.
Exemplo 2
Verifique se x5 – 2x4 + x3 + x – 2 é divisível por x – 1.
Segundo D’Alembert, um polinômio é divisível por um binômio se P(a) = 0.
P(1) = (1)5 – 2*(1)4 + (1)3 + (1) – 2
P(1) = 1 – 2 + 1 + 1 – 2
P(1) = 3 – 4
P(1) = – 1
Como P(1) é diferente de zero, o polinômio não será divisível pelo binômio x – 1.
Exemplo 3
Calcule o valor de m de modo que o resto da divisão do polinômio
P(x) = x4 – mx3 + 5x2 + x – 3 por x – 2 seja 6.
Temos que, R = P(x) → R = P(2) → P(2) = 6
P(2) = 24 – m*23 + 5*22 + 2 – 3
24 – m*23 + 5*22 + 2 – 3 = 6
16 – 8m + 20 + 2 – 3 = 6
– 8m = 6 – 38 + 3
– 8m = 9 – 38
– 8m = – 29
m = 29/8
Exemplo 4
Calcule o resto da divisão do polinômio 3x3 + x2 – 6x + 7 por 2x + 1.
R = P(x) → R = P(– 1/2)
R = 3*(–1/2)3 + (–1/2)2 – 6*(–1/2) + 7
R = 3*(–1/8) + 1/4 + 3 + 7
R = –3/8 + 1/4 + 10 (mmc)
R = –3/8 + 2/8 + 80/8
R = 79/8
x = a. O matemático francês D’Alembert provou, levando em consideração o teorema citado acima, que um polinômio qualquer Q(x) será divisível por x – a, ou seja, o resto da divisão será igual à zero (R = 0) se P(a) = 0.
Esse teorema facilitou o cálculo da divisão de polinômio por binômio (x –a), dessa forma não sendo preciso resolver toda a divisão para saber se o resto é igual ou diferente de zero.
Exemplo 1
Calcule o resto da divisão (x2 + 3x – 10) : (x – 3).
Como diz o Teorema de D’Alembert, o resto (R) dessa divisão será igual a:
P(3) = R
32 + 3 * 3 – 10 = R
9 + 9 – 10 = R
18 – 10 = R
R = 8
Portanto, o resto dessa divisão será 8.
Exemplo 2
Verifique se x5 – 2x4 + x3 + x – 2 é divisível por x – 1.
Segundo D’Alembert, um polinômio é divisível por um binômio se P(a) = 0.
P(1) = (1)5 – 2*(1)4 + (1)3 + (1) – 2
P(1) = 1 – 2 + 1 + 1 – 2
P(1) = 3 – 4
P(1) = – 1
Como P(1) é diferente de zero, o polinômio não será divisível pelo binômio x – 1.
Exemplo 3
Calcule o valor de m de modo que o resto da divisão do polinômio
P(x) = x4 – mx3 + 5x2 + x – 3 por x – 2 seja 6.
Temos que, R = P(x) → R = P(2) → P(2) = 6
P(2) = 24 – m*23 + 5*22 + 2 – 3
24 – m*23 + 5*22 + 2 – 3 = 6
16 – 8m + 20 + 2 – 3 = 6
– 8m = 6 – 38 + 3
– 8m = 9 – 38
– 8m = – 29
m = 29/8
Exemplo 4
Calcule o resto da divisão do polinômio 3x3 + x2 – 6x + 7 por 2x + 1.
R = P(x) → R = P(– 1/2)
R = 3*(–1/2)3 + (–1/2)2 – 6*(–1/2) + 7
R = 3*(–1/8) + 1/4 + 3 + 7
R = –3/8 + 1/4 + 10 (mmc)
R = –3/8 + 2/8 + 80/8
R = 79/8

otimo muito boom!
ResponderExcluirOLA PROFº COMO ENCONTO A PARA QUE 1 SEJA RAIZ Q(X)=2x4-2x3+ax (2-) 6x-8.
ResponderExcluirSubstitui no lugar de x o valor 1 e encontra o valor de a
Excluircomo resolvo essa equação algébrica 2.x²-x+3 sabendo que o x=1/3?
ResponderExcluirBoa noite ! Como eu resolvo essa questao : [Q (x)] ao cubo , calcule sabendo que Q(x)=x - 1 ... ?
ResponderExcluirBoa Noite, como resolvo a questão seguinte "(4x³ -12x² +19x -15) / (2x -3) e, em seguida, calcule o valor numérico desse quociente se x= -0,2."
ResponderExcluircomo calculo essa questao 1+2x+3x²+4x³+...-1<x<1
ResponderExcluircomo resolvo esta questão. podem me ajudar por favor.
ResponderExcluirCalcule a divisão pelo método de chave entre o polinômio – 3x³ - 2x² + x – 1 e o binômio x – 1.
olá , quero saber que equação do 2 grau chegas as raízes 2 e -3
ResponderExcluirPrezados Gostaria de saber como resolver a seguinte equação:
ResponderExcluira) (x³+x²-3x+5):(x-1)=
b)(x³+2x²-4):(x-2)=
Este comentário foi removido pelo autor.
ExcluirEste comentário foi removido pelo autor.
Excluircomo resolvo: x²-2x+1/x-36 : x-1/x+6
ResponderExcluir(x^2 - 2x +1/x-36 ) . (x+6/x-1) =x^3+4x^2-11x+6/(x-36)(x-1) e assim por diante
Excluircomo eu faço o quociente de ( x² + 5x + 6) : (x + 2) ?
ResponderExcluiraguem pode me ajudar com esse exercicio X^4+2x³-2x²-4x-21 por x+3
ResponderExcluirX^4 e elevado a quarta
Preciso urgentemente ajuda na questão: No polinomio p(x)=x^n+1+ x^n+x^n-1.........x^2+x+1,n é par e maior que 2. Assim o valor da expressão 2p(-1)+p(1)-1 é:
ResponderExcluirBem legal, bem bom !! Gostei !!
ResponderExcluirMas uma forma bem mais resumida seria bem interessante. Se bem que este assunto não dá pra resumir muito.
Mas algo tipo um cola, na hora da prova, como se fosse assim !
A regra e o que é... Algo para nunca esquecer mesmo.
Mas eu gostei, pra quem quer pegar parte por parte é um ótimo site !!
Parabéns, ao criador !!
Muito bom... Mas sugiro que façam em outra pagina também algo bem resumido, pra quem já aprendeu, e quer só relembrar. Nota 10 mesmo.
E apenas sugeri isso, porque a capacidade já foi grande, para fazer isso. Então não custa fazer outra resumindo o assunto por completo.
Ajudou muito !!
Ótimo !!
gostei ,, mi salvou numa prova que vou fazer!
ResponderExcluirpolinomios sendo p (x)=7x-8x+6x-5x+10 Q (x) = x+4 G(x) 3x+2x+4x+x+1
ResponderExcluircalcular o resultado da divisão de polinomios usando a fatoração:
ResponderExcluirx^3-27/3-x? me ajunde ai
Oi professor como eu resolvo essa conta p(x)=(4x²-2x+5)³.
ResponderExcluirOi professor como eu resolvo essa conta p(x)=(4x²-2x+5)³.
ResponderExcluirmultiplicação de grau de polinomio
ResponderExcluircomo resolvo a soma dos coeficientes da segunda derivada da f(x)= x^4-5x^3+3x^2-6x+10
ResponderExcluirComo eu respondo essa conta 8x ao quadrado +6x+5 ÷ por 2x +1????
ResponderExcluirComo eu respondo essa conta 8x ao quadrado +6x+5 ÷ por 2x +1????
ResponderExcluirComo resulvo este exercicio
ResponderExcluirZ^3-2Z^2+17Z-15
Factorize o polinomio sob forna de produto de factores lineares.
Como resolver x³+3x²-2x³+x²
ResponderExcluirboa tarde como desenvolver produto de factores lineares o polinómio de z?
ResponderExcluirSe eu tenho X⁴+3x²+x+3=0 como posso resolver de forma rápida?
ResponderExcluircomo resolvo a questão: Dada a função f(x)=-5x+3 sobre raiz quadrada de 2x+1, Calcular o valor numérico de: f(0), f(3), f(-2) e f(5).
ResponderExcluirDada a função: g(x)=2x4-5x3=2x2=2x=1, calcular o valor numérico de: g(0), g(2), g(-2) e g(5).
ResponderExcluirCOMO RESOLVER dividindo p(x)por d(x)=x2+1 ENCONTRE q(x)=-7-11
ResponderExcluirTenho dúvida se 8 / 2 *(2 * 2) ser 1 ou 16
ResponderExcluirCalcule a e b no
ResponderExcluirpolinômio f(x) = x3 + 2x2 + ax + b,
de modo que f(x) + 1 seja
divisível porx +1 e f(x)-1 seja
divisível por x-1.