Introdução à estatística
1- Objeto da estatística
Estatística é uma ciência exata que visa fornecer subsídios ao analista para coletar, organizar, resumir, analisar e apresentar dados. Trata de parâmetros extraídos da população, tais como média ou desvio padrão.
A estatística fornece-nos as técnicas para extrair informação de dados, os quais são muitas vezes incompletos, na medida em que nos dão informação útil sobre o problema em estudo, sendo assim, é objetivo da Estatística extrair informação dos dados para obter uma melhor compreensão das situações que representam.
Quando se aborda uma problemática envolvendo métodos estatísticos, estes devem ser utilizados mesmo antes de se recolher a amostra, isto é, deve-se planejar a experiência que nos vai permitir recolher os dados, de modo que, posteriormente, se possa extrair o máximo de informação relevante para o problema em estudo, ou seja para a população de onde os dados provêm.
Quando de posse dos dados, procura-se agrupa-los e reduzi-los, sob forma de amostra, deixando de lado a aleatoriedade presente.
Seguidamente o objetivo do estudo estatístico pode ser o de estimar uma quantidade ou testar uma hipótese, utilizando-se técnicas estatísticas convenientes, as quais realçam toda a potencialidade da Estatística, na medida em que vão permitir tirar conclusões acerca de uma população, baseando-se numa pequena amostra, dando-nos ainda uma medida do erro cometido.
Exemplo 1:
Ao chegarmos a uma churrrascaria, não precisamos comer todos os tipos de saladas, de sobremesas e de carnes disponíveis, para conseguirmos chegar a conclusão de que a comida é de boa qualidade. Basta que seja provado um tipo de cada opção para concluirmos que estamos sendo bem servidos e que a comida está dentro dos padrões.
2- População e amostra
Qualquer estudo científico enfrenta o dilema de estudo da população ou da amostra. Obviamente tería-se uma precisão muito superior se fosse analisado o grupo inteiro, a população, do que uma pequena parcela representativa, denominada amostra. Observa-se que é impraticável na grande maioria dos casos, estudar-se a população em virtude de distâncias, custo, tempo, logística, entre outros motivos.
A alternativa praticada nestes casos é o trabalho com uma amostra confiável. Se a amostra é confiável e proporciona inferir sobre a população, chamamos de inferência estatística. Para que a inferência seja válida, é necessária uma boa amostragem, livre de erros, tais como falta de determinação correta da população, falta de aleatoriedade e erro no dimensionamento da amostra.
Quando não é possível estudar, exaustivamente, todos os elementos da população, estudam-se só alguns elementos, a que damos o nome de Amostra.
Exemplo 2:
Se o objetivo for estudar o desempenho escolar de um colégio, é indicado estudar as notas dos alunos ao final do ano letivo. A partir daí poderemos facilmente obter a percentagem de aprovações e reprovações.
Agora, se entretanto o interesse for aprofundar o estudo, saber se por exemplo o sucesso no estudo pode ser atribuído para as alunas ou alunos, deveremos recolher não somente a informação relativa a nota do aluno que aprovou ou não, mas também para cada um, o sexo.
| Aprovados | |
| Masculino | 28% |
| Feminino | 13% |
| Total | 41% |
Quando a amostra não representa corretamente a população diz-se enviesada e a sua utilização pode dar origem a interpretações erradas.
3- Recenseamento
Recenseamento é a contagem oficial e periódica dos indivíduos de um País, ou parte de um País. Ele abrange, no entanto, um leque mais vasto de situações. Assim, pode definir-se recenseamento do seguinte modo:
Estudo científico de um universo de pessoas, instituições ou objetos físicos com o propósito de adquirir conhecimentos, observando todos os seus elementos, e fazer juízos quantitativos acerca de características importantes desse universo.
4- Estatística descritiva e estatística indutiva
Sondagem
Por vezes não é viável nem desejável, principalmente quando o número de elementos da população é muito elevado, inquirir todos os seus elementos sempre que se quer estudar uma ou mais características particulares dessa população.
Assim surge o conceito de sondagem, que se pode tentar definir como:
Estudo científico de uma parte de uma população com o objetivo de estudar atitudes, hábitos e preferências da população relativamente a acontecimentos, circunstâncias e assuntos de interesse comum.
5- Amostragem
Amostragem é o processo que procura extrair da população elementos que através de cálculos probabilísticos ou não, consigam prover dados inferenciais da população-alvo.
| Tipos de Amostragem | Não Probabilística |
| Acidental ou conveniência | |
| Intencional | |
| Quotas ou proporcional | |
| Desproporcional | |
| Probabilística | |
| Aleatória Simples | |
| Aleatória Estratificada | |
| Conglomerado |
Não Probabilística
A escolha de um método não probabilístico, via de regra, sempre encontrará desvantagem frente ao método probabilístico. No entanto, em alguns casos, se faz necessário a opção por este método. Fonseca (1996), alerta que não há formas de se generalizar os resultados obtidos na amostra para o todo da população quando se opta por este método de amostragem.
5.1- Acidental ou conveniência
Indicada para estudos exploratórios. Freqüentemente utilizados em super mercados para testar produtos.
Intencional
O entrevistador dirige-se a um grupo em específico para saber sua opinião. Por exemplo, quando de um estudo sobre automóveis, o pesquisador procura apenas oficinas.
5.2- Quotas ou proporcional
Na realidade, trata-se de uma variação da amostragem intencional. Necessita-se ter um prévio conhecimento da população e sua proporcionalidade. Por exemplo, deseja-se entrevistar apenas indivíduos da classe A, que representa 12% da população. Esta será a quota para o trabalho. Comumente também substratifica-se uma quota obedecendo a uma segunda proporcionalidade.
5.3- Desproporcional
Muito utilizada quando a escolha da amostra for desproporcional à população. Atribui-se pesos para os dados, e assim obtém-se resultados ponderados representativos para o estudo.
Exemplo 3:
Em um mercado de telefones celulares, considerando uma fatia de mercado meramente ilustrativa, obteve-se os resultados conforme descritos a seguir:
| Marcas | Participação no mercado | Elementos da Amostra | |
| n | % | ||
| Nokia | 60% | 50 | 25% |
| Ericson | 20% | 50 | 25% |
| Gradiente | 15% | 50 | 25% |
| Philips | 05% | 50 | 25% |
| Total | 100% | 200 | 100% |
Objetivando obtermos os pesos a serem atribuídos a cada marca de telefone celular, para uma análise conjunta de todas as marcas no exemplo acima, obtemos os seguintes coeficientes:
| Marcas | Pesos | Número de elementos a serem entrevistados |
| Nokia | 2,4 | 120 |
| Ericson | 0,8 | 40 |
| Gradiente | 0,6 | 30 |
| Philips | 0,2 | 10 |
| Total | 4,0 | 200 |
Probabilística
Para que se possa realizar inferências sobre a população, é necessário que se trabalhe com amostragem probabilística. É o método que garante segurança quando investiga-se alguma hipótese. Normalmente os indivíduos investigados possuem a mesma probabilidade de ser selecionado na amostra.
5.4- Aleatória Simples
É o mais utilizado processo de amostragem. Prático e eficaz, confere precisão ao processo de amostragem. Normalmente utiliza-se uma tabela de números aleatórios e nomeia-se os indivíduos, sorteando-se um por um até completar a amostra calculada
Uma variação deste tipo de amostragem é a sistemática. Em um grande número de exemplos, o pesquisador depara-se com a população ordenada. Neste sentido, tem-se os indivíduos dispostos em seqüência o que dificulta a aplicação exata desta técnica.
Quando se trabalha com sorteio de quadras de casas por exemplo, há uma regra crescente para os números das casas. Em casos como este, divide-se a população pela amostra e obtém-se um coeficiente (y). A primeira casa será a de número x, a segunda será a de número x + y; a terceira será a de número x + 3. y.
Supondo que este coeficiente seja 6. O primeiro elemento será 3. O segundo será 3 + 6. O terceiro será 3 + 2.6. O quarto será 3 + 3.6, e assim sucessivamente.
Aleatória Estratificada
Quando se deseja guardar uma proporcionalidade na população heterogênea. Estratifica-se cada subpopulação por intermédio de critérios como classe social, renda, idade, sexo, entre outros.
5.5- Conglomerado
Em corriqueiras situações, torna-se difícil coletar características da população. Nesta modalidade de amostragem, sorteia-se um conjunto e procura-se estudar todo o conjunto. É exemplo de amostragem por conglomerado, famílias, organizações e quarteirões.
6- Dimensionamento da amostra
Quando deseja-se dimensionar o tamanho da amostra, o procedimento desenvolve-se em três etapas distintas:
-
Avaliar a variável mais importante do grupo e a mais significativa;
-
Analisar se é ordinal, intervalar ou nominal;
-
Verificar se a população é finita ou infinita;
| Variável intervalar e população infinita | |
| Variável intervalar e população finita | |
| Variável nominal ou ordinal e população infinita | |
| Variável nominal ou ordinal e população finita |
Obs.: A proporção (p) será a estimativa da verdadeira proporção de um dos níveis escolhidos para a variável adotada. Por exemplo, 60% dos telefones da amostra é Nokia, então p será 0,60.
A proporção (q) será sempre 1 - p. Neste exemplo q, será 0,4. O erro é representado por d.
Para casos em que não se tenha como identificar as proporções confere-se 0,5 para p e q.
7- Tipos de dados
Basicamente os dados, dividem-se em contínuos e discretos. O primeiro é definido como qualquer valor entre dois limites quaisquer, tal como um diâmetro. Portanto trata-se de um valor que ser "quebrado". São dados contínuos, questões que envolvem idade, renda, gastos, vendas, faturamento, entre muitas outras.
Quando fala-se em valores discretos, aborda-se um valor exato, tal como quantidade de peças defeituosas. Comumente utiliza-se este tipo de variáveis para tratar de numero de filhos, satisfação e escalas nominais no geral.
O tipologia dos dados determina a variável, ela será portanto contínua ou discreta. Isto quer dizer que ao definir-se uma variável com contínua ou discreta, futuramente já definiu-se que tipo de tratamento se dará a ela.
De acordo com o que dissemos anteriormente, numa análise estatística distinguem-se essencialmente duas fases:
Uma primeira fase em que se procura descrever e estudar a amostra:
Estatística Descritiva e uma segunda fase em que se procura tirar conclusões para a população:
1ª Fase Estatística Descritiva
Procura-se descrever a amostra, pondo em evidência as características principais e as propriedades.
2ª Fase Estatística Indutiva
Conhecidas certas propriedades (obtidas a partir de uma análise descritiva da amostra), expressas por meio de proposições, imaginam-se proposições mais gerais, que exprimam a existência de leis (na população).
No entanto, ao contrário das proposições deduzidas, não podemos dizer que são falsas ou verdadeiras, já que foram verificadas sobre um conjunto restrito de indivíduos, e portanto não são falsas, mas não foram verificadas para todos os indivíduos da População, pelo que também não podemos afirmar que são verdadeiras !
Existe, assim, um certo grau de incerteza (percentagem de erro) que é medido em termos de Probabilidade.
Considerando o que foi dito anteriormente sobre a Estatística Indutiva, precisamos aqui da noção de Probabilidade, para medir o grau de incerteza que existe, quando tiramos uma conclusão para a população, a partir da observação da amostra.
Exemplo 4:
Uma empresa fabricante de um automóvel, pretende avaliar a potencialidade do mercado, estimando através de um mercado teste.Através de1000 entrevistados, pretende-se verificar como se comportará a fatia de intenção de votos para determinado candidato.
Problema: pretende-se, a partir da percentagem de respostas afirmativas, de entre os inquiridos sobre a compra do novo produto, obter uma estimativa do número de compradores na População.
8- Dados, tabelas e gráficos
Distribuição de freqüência
Quando da análise de dados, é comum procurar conferir certa ordem aos números tornando-os visualmente mais amigáveis. O procedimento mais comum é o de divisão por classes ou categorias, verificando-se o número de indivíduos pertencentes a cada classe.
1. Determina-se o menor e o maior valor para o conjunto:
2. Definir o limite inferior da primeira classe (Li) que deve ser igual ou ligeiramente inferior ao menor valor das observações:
3. Definir o limite superior da última classe (Ls) que deve ser igual ou ligeiramente superior ao maior valor das observações:
4. Definir o número de classes (K), que será calculado usando ![]() . Obrigatoriamente deve estar compreendido entre 5 a 20.
. Obrigatoriamente deve estar compreendido entre 5 a 20.
5. Conhecido o número de classes define-se a amplitude de cada classe:
6. Com o conhecimento da amplitude de cada classe, define-se os limites para cada classe (inferior e superior)
Exemplo 5:
| 5,1 | 5,3 | 5,3 | 5,6 | 5,8 | 5,9 | 6 | 6,1 | 6,2 | 6,2 |
| 6,3 | 6,3 | 6,3 | 6,4 | 6,4 | 6,4 | 6,5 | 6,5 | 6,6 | 6,7 |
| 6,7 | 6,8 | 6,8 | 6,9 | 6,9 | 7 | 7,1 | 7,1 | 7,2 | 7,2 |
| 7,3 | 7,4 | 7,5 | 7,5 | 7,6 | 7,6 | 7,6 | 7,7 | 7,7 | 7,8 |
| 7,8 | 7,9 | 7,9 | 8 | 8 | 8,1 | 8,2 | 8,3 | 8,4 | 8,5 |
| 8,5 | 8,6 | 8,7 | 8,8 | 8,9 | 8,9 | 9 | 9,1 | 9,2 | 9,4 |
| 9,4 | 9,5 | 9,5 | 9,6 | 9,8 | 9 | 9 | 10 | 10,2 | 10,2 |
| 10,4 | 10,6 | 10,8 | 10,9 | 11,2 | 11,5 | 11,8 | 12,3 | 12,7 | 14,9 |
Regras para elaboração de uma distribuição de freqüências
1. Determina-se o menor e o maior valor para o conjunto:
Valor mínimo: 5,1
Valor máximo: 14,9
2. Definir o limite inferior da primeira classe (Li) que deve ser igual ou ligeiramente inferior ao menor valor das observações:
LI: 5,1
3. Definir o limite superior da última classe (Ls) que deve ser igual ou ligeiramente superior ao maior valor das observações:
LS:15
4. Definir o número de classes (K), que será calculado usando ![]() . Obrigatoriamente deve estar compreendido entre 5 a 20. Neste caso, K é igual a 8,94, aproximadamente, 8.
. Obrigatoriamente deve estar compreendido entre 5 a 20. Neste caso, K é igual a 8,94, aproximadamente, 8.
5. Conhecido o número de classes define-se a amplitude de cada classe:![]()
No exemplo, a será igual a:
1,23
6. Com o conhecimento da amplitude de cada classe, define-se os limites para cada classe (inferior e superior), onde limite Inferior será 5,1 e o limite superior será 15 + 1,23.
| Intervalo de Classe | Freqüência Absoluta | Freqüência Acumulada | Freqüência Relativa |
| 05,10 a 06,33 | 13 | 13 | 16,25% |
| 06,34 a 07,57 | 21 | 34 | 26,25% |
| 07,58 a 08,81 | 22 | 56 | 27,50% |
| 08,82 a 10,05 | 15 | 71 | 18,75% |
| 10,06 a 11,29 | 4 | 75 | 5,00% |
| 11,30 a 12,53 | 3 | 78 | 3,75% |
| 12,54 a 13,77 | 1 | 79 | 1,25% |
| 13,78 a 15,01 | 1 | 80 | 1,25% |
| | 80 | | 100% |
Distribuições simétricas
A distribuição das frequências faz-se de forma aproximadamente simétrica, relativamente a uma classe média
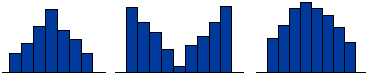
Caso especial de uma distribuição simétrica
Quando dizemos que os dados obedecem a uma distribuição normal, estamos tratando de dados que distribuem-se em forma de sino.
Distribuições Assimétricas
A distribuição das freqüências apresenta valores menores num dos lados:
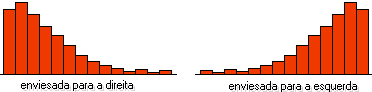
Distribuições com "caudas" longas
Observamos que nas extremidades há uma grande concentração de dados em relação aos concentrados na região central da distribuição.

9- Medidas de tendência Central
As mais importante medidas de tendência central, são a média aritmética, média aritmética para dados agrupados, média aritmética ponderada, mediana, moda, média geométrica, média harmônica, quartis. Quando se estuda variabilidade, as medidas mais importantes são: amplitude, desvio padrão e variância.
| Medidas | |
| Média aritmética | |
| Média aritmética para dados agrupados | |
| Média aritmética ponderada | |
| Mediana | 1) Se n é impar, o valor é central, 2) se n é par, o valor é a média dos dois valores centrais |
| Moda | Valor que ocorre com mais freqüência. |
| Média geométrica | |
| Média harmônica | |
| Quartil |
Sendo a média uma medida tão sensível aos dados, é preciso ter cuidado com a sua utilização, pois pode dar uma imagem distorcida dos dados.
Pode-se mostrar, que quando a distribuição dos dados é "normal", então a melhor medida de localização do centro, é a média.
Sendo a Distribuição Normal uma das distribuições mais importantes e que surge com mais freqüência nas aplicações, (esse fato justifica a grande utilização da média).
A média possui uma particularidadebastante interessante, que consiste no seguinte:
se calcularmos os desvios de todas as observações relativamente à média e somarmos esses desvios o resultado obtido é igual a zero.
A média tem uma outra característica, que torna a sua utilização vantajosa em certas aplicações:
Quando o que se pretende representar é a quantidade total expressa pelos dados, utiliza-se a média.
Na realidade, ao multiplicar a média pelo número total de elementos, obtemos a quantidade pretendida.
9.1- Moda
Define-se moda como sendo: o valor que surge com mais freqüência se os dados são discretos, ou, o intervalo de classe com maior freqüência se os dados são contínuos.
Assim, da representação gráfica dos dados, obtém-se imediatamente o valor que representa a moda ou a classe modal
Esta medida é especialmente útil para reduzir a informação de um conjunto de dados qualitativos, apresentados sob a forma de nomes ou categorias, para os quais não se pode calcular a média e por vezes a mediana.
9.2- Mediana
A mediana, é uma medida de localização do centro da distribuição dos dados, definida do seguinte modo:
Ordenados os elementos da amostra, a mediana é o valor (pertencente ou não à amostra) que a divide ao meio, isto é, 50% dos elementos da amostra são menores ou iguais à mediana e os outros 50% são maiores ou iguais à mediana
Para a sua determinação utiliza-se a seguinte regra, depois de ordenada a amostra de n elementos:
Se n é ímpar, a mediana é o elemento médio.
Se n é par, a mediana é a semi-soma dos dois elementos médios.
9.3-Considerações a respeito de Média e Mediana
Se se representarmos os elementos da amostra ordenada com a seguinte notação: X1:n , X2:n , ... , Xn:n
então uma expressão para o cálculo da mediana será:
Como medida de localização, a mediana é mais robusta do que a média, pois não é tão sensível aos dados.
1- Quando a distribuição é simétrica, a média e a mediana coincidem.
2- A mediana não é tão sensível, como a média, às observações que são muito maiores ou muito menores do que as restantes (outliers). Por outro lado a média reflete o valor de todas as observações.
Como já vimos, a média ao contrário da mediana, é uma medida muito influenciada por valores "muito grandes" ou "muito pequenos", mesmo que estes valores surjam em pequeno número na amostra. Estes valores são os responsáveis pela má utilização da média em muitas situações em que teria mais significado utilizar a mediana.
A partir do exposto, deduzimos que se a distribuição dos dados:1. for aproximadamente simétrica, a média aproxima-se da mediana
2. for enviesada para a direita (alguns valores grandes como "outliers"), a média tende a ser maior que a mediana
3. for enviesada para a esquerda (alguns valores pequenos como "outliers"), a média tende a ser inferior à mediana.
10 - Medidas de dispersão
Introdução
No capítulo anterior, vimos algumas medidas de localização do centro de uma distribuição de dados. Veremos agora como medir a variabilidade presente num conjunto de dados através das seguintes medidas:
10.1- Medidas de dispersão
Um aspecto importante no estudo descritivo de um conjunto de dados, é o da determinação da variabilidade ou dispersão desses dados, relativamente à medida de localização do centro da amostra.
Supondo ser a média, a medida de localização mais importante, será relativamente a ela que se define a principal medida de dispersão - a variância, apresentada a seguir.
10.2- Variância
Define-se a variância, como sendo a medida que se obtém somando os quadrados dos desvios das observações da amostra, relativamente à sua média, e dividindo pelo número de observações da amostra menos um.
![]()
10.3- Desvio-padrão
Uma vez que a variância envolve a soma de quadrados, a unidade em que se exprime não é a mesma que a dos dados. Assim, para obter uma medida da variabilidade ou dispersão com as mesmas unidades que os dados, tomamos a raiz quadrada da variância e obtemos o desvio padrão:
O desvio padrão é uma medida que só pode assumir valores não negativos e quanto maior for, maior será a dispersão dos dados.
Algumas propriedades do desvio padrão, que resultam imediatamente da definição, são:
o desvio padrão será maior, quanta mais variabilidade houver entre os dados.
![]()
Exemplo 7:
Em uma turma de aluno, verificou-se através da análise das notas de 15 alunos, os seguintes desempenhos:
| Alunos | Conceito na Prova |
| 1 | 4,3 |
| 2 | 4,5 |
| 3 | 9 |
| 4 | 6 |
| 5 | 8 |
| 6 | 6,7 |
| 7 | 7,5 |
| 8 | 10 |
| 9 | 7,5 |
| 10 | 6,3 |
| 11 | 8 |
| 12 | 5,5 |
| 13 | 9,7 |
| 14 | 9,3 |
| 15 | 7,5 |
| Total | 109,8 |
| Média | 7,32 |
| Desvio Padrão | 1,77 |
Observamos no exemplo, que a média das provas, foi estimada em 7,32 com desvio padrão em 1,77. Concluimos que a maioria das notas concentrou-se em 9,09 e 5,55.
11. Distribuição Normal
A distribuição normal é a mas importante distribuição estatística,
considerando a questão prática e teórica. Já vimos que esse tipo de distribuição apresenta-se em formato de sino, unimodal, simétrica em relação a sua média.
Considerando a probabilidade de ocorrência, a área sob sua curva soma 100%. Isso quer dizer que a probabilidade de uma observação assumir um valor entre dois pontos quaisquer é igual à área compreendida entre esses dois pontos.
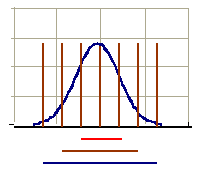
68,26% => 1 desvio
95,44% => 2 desvios
99,73% => 3 desvios
Na figura acima, tem as barras na cor marrom representando os desvios padrões. Quanto mais afastado do centro da curva normal, mais área compreendida abaixo da curva haverá. A um desvio padrão, temos 68,26% das observações contidas. A dois desvios padrões, possuímos 95,44% dos dados comprendidos e finalmente a três desvios, temos 99,73%. Podemos concluir que quanto maior a variablidade dos dados em relação à média, maior a probabilidade de encontrarmos o valor que buscamos embaixo da normal.
Propriedade 1:
"f(x) é simétrica em relação à origem, x = média = 0;
Propriedade 2:
"f(x) possui um máximo para z=0, e nesse caso sua ordenada vale 0,39;
Propriedade3:
"f(x) tende a zero quando x tende para + infinito ou - infinito;
Propriedade4:
"f(x) tem dois pontos de inflexão cujas abscissas valem média + DP e média - DP, ou quando z tem dois pontos de inflexão cujas abscissas valem +1 e -1.
Para se obter a probabilidade sob a curva normal, utilizamos a tabela de faixa central
Tabela normal
(distribuição z)
| z | .00 | .01 | .02 | .03 | .04 | .05 | .06 | .07 | .08 | .09 |
| -4.0 | 0.00003 | 0.00003 | 0.00003 | 0.00003 | 0.00003 | 0.00003 | 0.00002 | 0.00002 | 0.00002 | 0.00002 |
| -3.9 | 0.00005 | 0.00005 | 0.00004 | 0.00004 | 0.00004 | 0.00004 | 0.00004 | 0.00004 | 0.00003 | 0.00003 |
| -3.8 | 0.00007 | 0.00007 | 0.00007 | 0.00006 | 0.00006 | 0.00006 | 0.00006 | 0.00005 | 0.00005 | 0.00005 |
| -3.7 | 0.00011 | 0.00010 | 0.00010 | 0.00010 | 0.00009 | 0.00009 | 0.00008 | 0.00008 | 0.00008 | 0.00008 |
| -3.6 | 0.00016 | 0.00015 | 0.00015 | 0.00014 | 0.00014 | 0.00013 | 0.00013 | 0.00012 | 0.00012 | 0.00011 |
| -3.5 | 0.00023 | 0.00022 | 0.00022 | 0.00021 | 0.00020 | 0.00019 | 0.00019 | 0.00018 | 0.00017 | 0.00017 |
| -3.4 | 0.00034 | 0.00032 | 0.00031 | 0.00030 | 0.00029 | 0.00028 | 0.00027 | 0.00026 | 0.00025 | 0.00024 |
| -3.3 | 0.00048 | 0.00047 | 0.00045 | 0.00043 | 0.00042 | 0.00040 | 0.00039 | 0.00038 | 0.00036 | 0.00035 |
| -3.2 | 0.00069 | 0.00066 | 0.00064 | 0.00062 | 0.00060 | 0.00058 | 0.00056 | 0.00054 | 0.00052 | 0.00050 |
| -3.1 | 0.00097 | 0.00094 | 0.00090 | 0.00087 | 0.00084 | 0.00082 | 0.00079 | 0.00076 | 0.00074 | 0.00071 |
| -3.0 | 0.00135 | 0.00131 | 0.00126 | 0.00122 | 0.00118 | 0.00114 | 0.00111 | 0.00107 | 0.00103 | 0.00100 |
| -2.9 | 0.00187 | 0.00181 | 0.00175 | 0.00169 | 0.00164 | 0.00159 | 0.00154 | 0.00149 | 0.00144 | 0.00139 |
| -2.8 | 0.00256 | 0.00248 | 0.00240 | 0.00233 | 0.00226 | 0.00219 | 0.00212 | 0.00205 | 0.00199 | 0.00193 |
| -2.7 | 0.00347 | 0.00336 | 0.00326 | 0.00317 | 0.00307 | 0.00298 | 0.00289 | 0.00280 | 0.00272 | 0.00264 |
| -2.6 | 0.00466 | 0.00453 | 0.00440 | 0.00427 | 0.00415 | 0.00402 | 0.00391 | 0.00379 | 0.00368 | 0.00357 |
| -2.5 | 0.00621 | 0.00604 | 0.00587 | 0.00570 | 0.00554 | 0.00539 | 0.00523 | 0.00508 | 0.00494 | 0.00480 |
| -2.4 | 0.00820 | 0.00798 | 0.00776 | 0.00755 | 0.00734 | 0.00714 | 0.00695 | 0.00676 | 0.00657 | 0.00639 |
| -2.3 | 0.01072 | 0.01044 | 0.01017 | 0.00990 | 0.00964 | 0.00939 | 0.00914 | 0.00889 | 0.00866 | 0.00842 |
| -2.2 | 0.01390 | 0.01355 | 0.01321 | 0.01287 | 0.01255 | 0.01222 | 0.01191 | 0.01160 | 0.01130 | 0.01101 |
| -2.1 | 0.01786 | 0.01743 | 0.01700 | 0.01659 | 0.01618 | 0.01578 | 0.01539 | 0.01500 | 0.01463 | 0.01426 |
| -2.0 | 0.02275 | 0.02222 | 0.02169 | 0.02118 | 0.02067 | 0.02018 | 0.01970 | 0.01923 | 0.01876 | 0.01831 |
| -1.9 | 0.02872 | 0.02807 | 0.02743 | 0.02680 | 0.02619 | 0.02559 | 0.02500 | 0.02442 | 0.02385 | 0.02330 |
| -1.8 | 0.03593 | 0.03515 | 0.03438 | 0.03362 | 0.03288 | 0.03216 | 0.03144 | 0.03074 | 0.03005 | 0.02938 |
| -1.7 | 0.04456 | 0.04363 | 0.04272 | 0.04181 | 0.04093 | 0.04006 | 0.03920 | 0.03836 | 0.03754 | 0.03673 |
| -1.6 | 0.05480 | 0.05370 | 0.05262 | 0.05155 | 0.05050 | 0.04947 | 0.04846 | 0.04746 | 0.04648 | 0.04551 |
| -1.5 | 0.06681 | 0.06552 | 0.06425 | 0.06301 | 0.06178 | 0.06057 | 0.05938 | 0.05821 | 0.05705 | 0.05592 |
| -1.4 | 0.08076 | 0.07927 | 0.07780 | 0.07636 | 0.07493 | 0.07353 | 0.07214 | 0.07078 | 0.06944 | 0.06811 |
| -1.3 | 0.09680 | 0.09510 | 0.09342 | 0.09176 | 0.09012 | 0.08851 | 0.08691 | 0.08534 | 0.08379 | 0.08226 |
| -1.2 | 0.11507 | 0.11314 | 0.11123 | 0.10935 | 0.10749 | 0.10565 | 0.10383 | 0.10204 | 0.10027 | 0.09852 |
| -1.1 | 0.13566 | 0.13350 | 0.13136 | 0.12924 | 0.12714 | 0.12507 | 0.12302 | 0.12100 | 0.11900 | 0.11702 |
| -1.0 | 0.15865 | 0.15625 | 0.15386 | 0.15150 | 0.14917 | 0.14686 | 0.14457 | 0.14231 | 0.14007 | 0.13786 |
| -0.9 | 0.18406 | 0.18141 | 0.17878 | 0.17618 | 0.17361 | 0.17105 | 0.16853 | 0.16602 | 0.16354 | 0.16109 |
| -0.8 | 0.21185 | 0.20897 | 0.20611 | 0.20327 | 0.20045 | 0.19766 | 0.19489 | 0.19215 | 0.18943 | 0.18673 |
| -0.7 | 0.24196 | 0.23885 | 0.23576 | 0.23269 | 0.22965 | 0.22663 | 0.22363 | 0.22065 | 0.21769 | 0.21476 |
| -0.6 | 0.27425 | 0.27093 | 0.26763 | 0.26434 | 0.26108 | 0.25784 | 0.25462 | 0.25143 | 0.24825 | 0.24509 |
| -0.5 | 0.30853 | 0.30502 | 0.30153 | 0.29805 | 0.29460 | 0.29116 | 0.28774 | 0.28434 | 0.28095 | 0.27759 |
| -0.4 | 0.34457 | 0.34090 | 0.33724 | 0.33359 | 0.32997 | 0.32635 | 0.32276 | 0.31917 | 0.31561 | 0.31206 |
| -0.3 | 0.38209 | 0.37828 | 0.37448 | 0.37070 | 0.36692 | 0.36317 | 0.35942 | 0.35569 | 0.35197 | 0.34826 |
| -0.2 | 0.42074 | 0.41683 | 0.41293 | 0.40904 | 0.40516 | 0.40129 | 0.39743 | 0.39358 | 0.38974 | 0.38590 |
| -0.1 | 0.46017 | 0.45620 | 0.45224 | 0.44828 | 0.44433 | 0.44038 | 0.43644 | 0.43250 | 0.42857 | 0.42465 |
| -0.0 | 0.50000 | 0.49601 | 0.49202 | 0.48803 | 0.48404 | 0.48006 | 0.47607 | 0.47209 | 0.46811 | 0.46414 |
Exemplo 8:
As alturas de grupo de crianças são tidas como normais em sua distribuição, com desvio padrão em 0,30m e média em 1,60. Qual a probabilidade de um aluno medir (1) entre 1,50 e 1,80, (2) mais de 1,75 e menos de 1,48?
(1)
z1= (1,50-1,60)/0,30=-0,33
z2= (1,80-1,60)/0,30= 0,67
Então, z1 (0,1293) + z2 (0,2486) = 37,79%
(2)
z1= (1,75-1,60)/0,30=0,30
0,500-0,1915 = 30,85%
(3)
Z1= (1,48-1,50)/0,30 =-0,4
0,500-0,1554 = 34,46%
Exercícios
1. Supondo que a variável escolhida de um pesquisa, seja nominal e a população finita de 600 indivíduos (onde 60% dos indivíduos são mulheres). Deseja-se trabalhar com um alpha de 5% e um erro amostral de 7%. Calcule o tamanho da amostra.
2. Organize os dados abaixo em uma tabela de distribuição de freqüência, contendo o intervalo de classe, a freqüência absoluta, a freqüência acumulada, a freqüência relativa e a freqüência relativa acumulada.
| 20,4 | 22,3 | 23,1 | 23,5 | 23,8 | 24,1 | 24,3 | 24,3 | 24,6 |
| 26,0 | 25,0 | 25,1 | 25,3 | 25,3 | 25,4 | 25,6 | 25,7 | 25,8 |
| 26,0 | 26,1 | 26,2 | 26,2 | 26,3 | 26,5 | 26,6 | 26,7 | 26,8 |
| 27,1 | 27,1 | 27,3 | 25,7 | 27,7 | 27,9 | 28,0 | 28,3 | 28,7 |
3. Três arremessadores de disco, treinam para a Olimpíada. Os atletas arremessam seus discos a 66 metros de distância (em média), com desvio padrão de 6,1 metros.
Qual a probabilidade de um atleta lançar seu disco entre 64 e 67 metros?
4. Foi encomendado um estudo para avaliação de uma entidade de ensino superior. Para isso, aplicou-se um questionário e obteve-se respostas de 110 alunos.
Indique:
a) a variável em estudo;
c) a população em estudo;
b) a amostra escolhida;
5. Indique abaixo quais amostras são consideradas boas:
a) Em um cinema, desejou-se verificar quais eram as intenções de voto para a próxima eleição. As pessoas entrevistadas, eram as que estavam presentes
b) Para saber a opinião a respeito de métodos contraceptivos, resolveu-se aplicar um estudo em uma escola de ensino fundamental, junto aos alunos.
5. Em uma pesquisa realizada em uma escola, identificou-se os seguintes indicadores
(1) idade
(2) anos de estudo
(3) ano de escolaridade
(4) renda
(5) sexo
(6) local de estudo
(7) conceito obtido na última prova de biologia
(8) Quantidade de livros que possui
a) Das variáveis acima, quais são as quantitativas e quais são as qualitativas?
b) Das variáveis quantitativas, diga quais são discretas?
6. Porque se realiza na Estatística, o estudo descritivo?
7. Num quartel, constatou-se que o peso médio de 40 soldados era de 69 Kilos. Posteriormente, verificou-se que a balança estava desregulada, ocasionando um peso indicado superior em 15 gramas ao peso verdadeiro. Qual era a média verdadeira dos pesos dos soldados?
8. Ao procurar emprego, um determinado cidadão, teve que optar por duas ofertas dispostas em um classificados. Qual a que representa a melhor opção? Porque?
| Oferta 1 | Oferta 2 | |
| Média Salarial | 890,00 | 950,00 |
| Mediana | 800,00 | 700,00 |
| Desvio Padrão | 32,00 | 38,00 |
9. Um produto pesa, em média, 10g, com desvio-padrão de 2 g. É embalado em caixas com 50 unidades. Sabe-se que as caixas vazias pesam 500g, com desvio-padrão de 25g. Admitindo-se uma distribuição normal dos pesos e independência entre as variáveis dos pesos do produto e da caixa, calcular a probabilidade de uma caixa cheia pesar mais de 1050g.
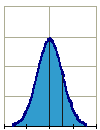
Utilize a figura acima para o desenvolvimento da questão, onde a primeira repartição, à direita, representa a probabilidade da caixa pesar 1050g.
Fonte: www.somatematica.com.br

cade a resposta
ResponderExcluirE a resolução? cadê???????
ResponderExcluirPosta a respostas seus fdps
ResponderExcluirSéria uma boa ideia a resolução dos exercícios
ResponderExcluir